Back in the Books
As discussed in my previous post, my boids weren't doing so hot. All because they were using a naive search algorithm which lead to a loop that would run n x (n - 1) cycles, where n is the number of boids. That meant that 10.000 boids would loop through 99.990.000 calculations, per frame. Though it should be said that it is still pretty impressive it can do that in 450ms that is unfortunately not enough to run an application in real time.
I thus had a clear job to do; reduce the number of cycles. To figure out the best way to do that, I dived into the online papers to see what the minds working on tomorrow have all come up with.
But first let's recap what the problem is. We are creating boids, and boids have certain behaviours. For every other boid that is inside their vision, they will adapt their movement to fall in line with the group (in most cases). That is why every boid needs to check if every other boid is inside their vision. The reason why we can't "just do that", is a question of what we see vs what the computer sees. Namely this:
The computer doesn't "have" vision, it has data. So in order to check if 2 points can see each other, we need to run some math operations on them. Since, to the computer, any point could be seeing any other point, we need to check all of them if we want an accurate result.
So how can we combat this? I found 3 ways, of which I will discuss the 3rd way first, because it is the most interesting as well as the least related to boid behaviours.
Way 3: Create Flocking Behaviour using Machine Learning
Definitely a recommendation if you are interested in this stuff is this paper here, which talks about how we can use machine learning agents trying to escape from a predator to display flocking behaviour, simply because it is their best strategy for survival. The real kicker is that these agents don't even need to know about each other in order to start flocking! While I definitely deeply wanted to try it for myself, machine learning is a whole other topic that I know nothing about, and I wanted a solution that I could implement in ECS, since that was what I was trying to focus on.
Way 1: Using Trees
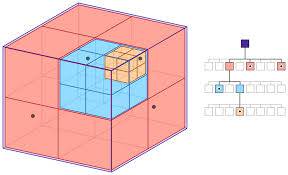
Trees do something clever, where they separate all of your points into their own little regions. So let's say we have 10 boids. 5 boids will be given to region A, and 5 boids will be given to region B. Now when a boid in region A needs to check what boids are inside its range of vision, it will ONLY check all the boids in region A. Coders will know this is a huge oversimplification, but generally that's the basic idea of it.
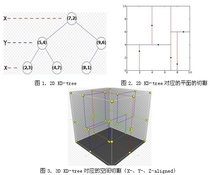
There are 2 implementations that I read about, which were the Octree and the k-d tree implementation. The octree divides a large, cubic region into smaller cubic regions. The k-d tree instead splits a cubic region up into different chunks that don't necessarily require to be cubic. The k-d tree seemed to me a bit more specialized when it game to divvying up clusters of boids, so that's the implementation I went with (also, not unrelated, I could find more examples of it.)
Way 2: Using Delaunay Triangulation
If you've never heard of Delaunay Triangulation; neither did I. And I'm still not quite sure how it works; but I do know what it does. It is typically used for mesh generation, because it can create a mesh (it's like a piece of computer-paper) out of a set of points, where the mesh doesn't overlap itself (a common problem in computer graphics) (image a book where the front and back cover are both drawn on the front, but it's mixed and mashed together like 2 different jigsaw puzzles and also flickers constantly) (yes, I'm not kidding, that's what it actually looks like).
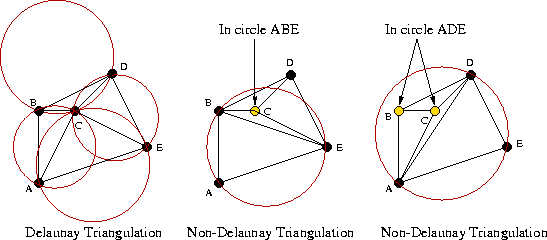
Now why is this useful for boids? Well, creating something out of a set of points... our boids are a set of points! All the happens when we use delaunay triangulation is that all our points get connected with lines. And those lines all have a distance! Basically, the created mesh "becomes" the computers visualization of our boids. All we have to do is loop through all of them and see which connecting lines are shorter than our boids range of vision and we have all their neighbors! (Actually we need to do some other operations as well but that would take another 2 paragraphs I know you're not waiting on).
The reason I did not take this approach was that I couldn't find any examples of this pattern being used for boids (except for 1 which only had like 50 boids in it). That's the second reason; I wasn't sure about the computational cost of this method. And the third, though I already said it twice: I STILL don't really understand how it works! Though I love to explore new subjects, exploring Delaunay Triangulation WHILST exploring how to do it in ECS... no thanks. I believe learning about one complicated subject at a time is a fair amount.
Dots Sandbox
Tests written with ECS to learn about Data Oriented Programming
| Status | In development |
| Category | Other |
| Author | Casey Hofland |
| Tags | dots, ecs, Physics, Unity |
More posts
- KDTree in ECSFeb 08, 2020
- Looking for Neighbors, Looking for TroubleJan 12, 2020
- First Jobs PrototypeJan 05, 2020
- Follow the processJan 05, 2020
Leave a comment
Log in with itch.io to leave a comment.